Fold kortet rigtigt sammen!

Kortfoldning, et tilsyneladende enkelt problem, viser sig som et dybt matematisk mysterium med uløste udfordringer. Det er et tilbagevendende tema i matematik med forbindelser til origami. Kernen i problemet lyder: "Givet et kort med M×N paneler, hvor mange unikke måder kan det foldes på?" To foldninger er kun ens, hvis de giver samme rækkefølge når du lægger det på bordet

 

Lodrette folder:

Den en-dimensionelle foldning

 

Det mest grundlæggende eksempel kunne være et lykønskningskort: et kort med kun to paneler, adskilt af en enkelt lodret fold.. Dette kan foldes på to måder: enten "korrekt", hvilket skaber en dal-fold (V), eller "forkert" med indersiden ud af, hvilket skaber en bjerg-fold (M). 

1 x 1 kort

3 x 1 kort

For et 3×1 kort, som mange foldere og brochurer med to lodrette folder, synes der umiddelbart at være otte måder at folde det på, hvis vi betragter hver fold som enten et bjerg (M) eller en dal (V). Men nogle af udfaldene er ens (ækvivalente), så vi ender på 6 unikke udfald.

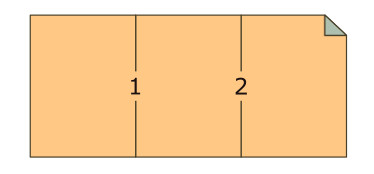
Bemærk, at rækkefølgen, hvori man starter med at folde, har betydning. Hvis vi begynder med fold 1 og dernæst fold 2, giver det 2 x 2 mulige udfald. Begynder vi derimod med fold 2 og derefter fold 1, opstår yderligere 2 x 2 mulige udfald.

Men når man undersøger de resulterende foldninger, opdager man, at nogle er ækvivalente på grund af symmetri eller ens lagrækkefølge. Specifikt er 1M-2V den samme foldning som 2V-1M, og 1V-2M er den samme som 2M-1V. Dette reducerer antallet af unikke måder at folde et 3×1 kort på til kun seks.

Kompleksiteten opstår herfra

Man kunne måske antage, at med N paneler skulle der være N! (N fakultet) måder at folde kort på, hvilket tilfældigvis stemmer overens med resultatet for N=3 (3! = 6).

Men som vi snart vil se, stemmer dette ikke altid. For eksempel, hvis der er fire paneler (4×1 kort), ville man forvente 4!=24 foldemønstre. I virkeligheden er der kun 16. Dette indikerer, at problemet er mere komplekst, end det umiddelbart ser ud.

Problemet med at folde et kort i dimensionen N×1 kaldes ofte frimærkefoldningsproblemet, da det gælder for lineære strimler af frimærker. Antallet af forskellige måder at folde en strimmel med N frimærker er en specifik talrække: 1,2,6,16,50,144,462,1392,4536,14060,46310,146376,485914,…. Dette er sekvens A000136 i Online Encyclopedia of Integer Sequences (OEIS). Mønsteret er langt fra indlysende. Selvom heuristiske metoder kan bruges til at estimere termer i denne række, kendes der ingen lukket formel, der effektivt kan udvide denne sekvens til meget store N-værdier. Problemet med at finde en sådan formel eller en algoritme, der effektivt kan tælle løsninger til frimærkefoldningsproblemet, er fortsat uløst.

---

 

Den To-Dimensionelle Verden: Kortfoldning

 

Når vi bevæger os op i en dimension, kan et kort have både lodrette og vandrette folder. For eksempel kan et 2×2 kort foldes på otte forskellige måder langs sine folder, hvor hver forskellig lodret sekvens af foldede paneler tælles som en særskilt måde at folde kortet på. Dette står i kontrast til den potentielle værdi L!, hvor L er det samlede antal paneler (L=M×N). For et 2×2 kort er L=4, så 4!=24. Imidlertid er mange af disse potentielle permutationer fysisk umulige at opnå på grund af den måde, panelerne er forbundet med hinanden. L! giver derfor kun en meget grov øvre grænse.

Man skelner mellem simple folder og komplekse foldemønstre. Simple folder betyder, at hver fold virker langs en fuld foldelinje, der strækker sig fra kant til kant. For et M×N kort er der M−1 lodrette fulde foldelinjer og N−1 vandrette fulde foldelinjer. Det samlede antal sådanne foldelinjer er n=(M−1)+(N−1)=M+N−2. For et 3×2 kort betyder dette n=3+2−2=3 foldelinjer. Da der er 3! = 6 måder at ordne folderne på, og hver fold kan være enten et bjerg eller en dal (2 muligheder), er der potentielt 3!×23=6×8=48 muligheder. Generelt er den øvre grænse for foldemønstre med n simple folder n!×2n. For et 5×5 kort er n=5+5−2=8 foldelinjer, og den øvre grænse er 8!×28=40.320×256=10.321.920.

Imidlertid findes der også talrige komplekse foldemønstre, hvor folder ikke nødvendigvis strækker sig over hele kortet. Man kan beregne det samlede antal foldesegmenter (creaselets), som er segmenter af en foldelinje mellem to tilstødende knudepunkter eller mellem et knudepunkt og kortets kant. For et M×N kort er der (M−1)N lodrette foldesegmenter og M(N−1) vandrette foldesegmenter. Det samlede antal foldesegmenter, K, er K=(M−1)N+M(N−1)=MN−N+MN−M=2MN−(M+N). Hvert foldesegment skal være enten et bjerg eller en dal. Derfor er den teoretiske øvre grænse for det samlede antal muligheder 2K. For et 2×2 kort er K=2(2×2)−(2+2)=8−4=4 foldesegmenter, og den øvre grænse er 24=16. Men som nævnt tidligere, er der i virkeligheden kun 8 gyldige mønstre. De resterende 8 udelukkes af en vigtig matematisk sætning:

Maekawas Sætning: Ved hvert knudepunkt (skæringspunkt mellem foldelinjer) på et fladt foldet stykke papir skal antallet af bjergfolder og dalfolder adskille sig med præcis to. I mere generelle tilfælde inden for origami betyder dette, at ved hvert knudepunkt er antallet af bjerge og dale altid ulige, og deres forskel er ±2. Denne sætning reducerer antallet af mulige løsninger betydeligt. For eksempel, for et 5×5 kort er K=2(5×5)−(5+5)=50−10=40 foldesegmenter, hvilket giver 240 mulige foldesegmentmønstre, eller omkring 1012. Men de fleste af disse fører ikke til en gyldig foldning; det faktiske antal foldemønstre er langt mindre end 2×109.

---

 

Et Fortsat Uløst Problem

 

Det generelle problem med at tælle antallet af måder at folde et M×N kort på forbliver uløst. Antallet af måder at folde et N×N kvadratisk kort på kendes kun for N≤7:

N1 = 1

N2 = 8

N3 = 1.368,

N4 = 300.608

N5 = 186.086.600

N6 = 123.912.532.224

129950723279272. Denne sekvens kan findes i OEIS som A001418. Dette problem er et aktivt uløst problem i matematik, hvor man endnu ikke kender en lukket formel eller en effektiv algoritme, der kan udvide disse sekvenser til meget store værdier af N.

At tælle kortfoldninger er utrolig tidskrævende. Et kort med 6×6 paneler kan foldes på 124 milliarder måder, og det tog en computer 16 minutter at beregne dette. For et 7×7 kort er antallet 130 billioner måder, og det ville tage en computer mellem 3 og 10 dage at beregne. Det højeste antal, mennesker hidtil har været i stand til at tælle for, er et 7×7 kort. For et 8×8 kort ville det tage en computer mellem 3 og 10 år at beregne alle foldninger. Dette illustrerer problemets enorme beregningsmæssige kompleksitet.

---

 

Forståelse af Foldbarhed og Repræsentationer

 

Et foldningsmønster beskriver ikke nødvendigvis en unik fysisk foldning, men hvis man tildeler et nummer til hvert segment, er der kun én måde at folde papiret på, så segmenterne er i den specificerede rækkefølge. Selvom det kan virke intuitivt at der skulle være N! permutationer for N paneler, stemmer dette sjældent. Den faktiske måde at tælle det nøjagtige antal foldninger på involverer en rekursiv proces, hvor man systematisk tilføjer et nyt panel i alle mulige "huller" i den eksisterende foldning. For at en computer effektivt kan håndtere disse beregninger, er det nødvendigt at bruge smarte repræsentationer af folder, f.eks. ved at anvende en liste af tal, hvor det i-te tal repræsenterer panelet umiddelbart efter panel i i den foldede stak.

For at tackle kompleksiteten af todimensionel kortfoldning er der udviklet særlige repræsentationer for 2×N kort, hvoraf den ene er "top-edge view". Dette visualiserer en flad foldet tilstand som en stak paneler, hvor hver celle repræsenteres af et vandret segment, og deres stakningsrækkefølge repræsenteres af lodret position. En anden, og ofte mere bekvem, repræsentation er "ray diagrammet". Ray diagrammet repræsenterer kortets "centerlinje" med en solid sort streg. De punkter, hvor foldelinjer mødes, kaldes knudepunkter. "Vest-" og "østknudepunkter" svarer til 180-graders drejninger i centerlinjen (altså punkter hvor papiret foldes fuldstændigt rundt om sig selv), mens "nord-" og "sydknudepunkter" ikke ændrer centerlinjens tunnelretning. Diagrammet kan indeholde "segments" (rene foldesegmenter) og "constrained segments" (foldesegmenter, der begrænser andre foldninger).

Et ray diagram er gyldigt, hvis det opfylder tre vigtige begrænsninger, der sikrer, at papiret ikke skærer sig selv:

• Centerlinjen må ikke skære sig selv. Hvis den gør det, svarer det til, at papiret skærer sig selv eller danner en lukket sløjfe.

• Nord- og sydstråler må kun skæres (lodret) af en stråle af matchende type. Dette betyder, at kun en nord-stråle kan passe inde i en anden nord-stråle på en anden "tunnel" (og tilsvarende for syd-stråler). Hvis en ydre tunnel har en nord- eller sydstråle, skal de indeholdte tunneler matche disse for at forhindre selv-skæring.

• Der skal være lighed mellem antallet af nord- og sydmarkører, der er synlige for et "constrained segment". Et "constrained segment" er et segment, hvis nedadgående projektion skærer andre segmenter. Denne betingelse sikrer, at tunnelens "tilstande" stemmer overens for at forhindre selv-skæring. En forskel i antallet af nord- og sydmarkører vil føre til, at den indre tunnel peger i den forkerte retning eller spiralerer ind i sig selv.

---

 

Algoritmer og Optimering

 

For 2×N kort er der udviklet en polynomiel-tids algoritme med en samlet køretid på O(N9). Denne algoritme opnås gennem en række reduktioner: fra 2×N kortfoldning til "top-edge view", derefter til "ray diagram", og til sidst til et problem kaldet "hidden tree problem". Det "hidden tree problem" løses effektivt ved hjælp af dynamisk programmering.

Der findes også hurtigere algoritmer for specialtilfælde af 2×N kortfoldning:

• Kort uden øst- eller vestknudepunkter (Kegleform): Disse kort er altid foldbare. Algoritmen tager O(1) tid.

• Kort med en enkelt vekslen mellem øst- og vestknudepunkter (Tænder): Denne type, der minder om "låsende tænder", kan løses med en dynamisk programmeringsalgoritme, der tager O(N5) tid. Hvis der ikke er nord- eller sydknudepunkter, kan det reduceres til O(N3) tid.

• Kort med skiftende øst- og vestknudepunkter (Spiral): Problemet med en enkelt spiral kan løses i O(N3) tid. For "dobbelte spiraler" (hvor sekvensen kan skifte mellem to spiraler), kan det samlede problem løses i O(N4) tid.

Derudover er der udviklet algoritmer til optimeringsproblemer inden for 2×N kortfoldning. I stedet for blot at bestemme, om en flad foldning eksisterer, kan man finde den "enkleste" foldning ud fra forskellige målestokke:

• Minimering af det samlede antal nord- og sydstråler, der er synlige for "constrained segments": Dette svarer heuristisk til at minimere "creep" (den maksimale foldning af papir inden for en enkelt foldelinje). Algoritmen tager O(N9) tid.

• Minimering af det maksimale antal nord- og sydstråler, der er synlige for et "constrained segment": Dette er mere beregningskrævende og kræver en modificeret træstruktur og dynamisk programmering, hvilket resulterer i en køretid på O(N15).

• Minimering af summen af nord- og syd-indlejringer: Dette fokuserer på at reducere "stablede" folder, hvor nord- og sydstråler skærer hinanden. Denne optimering kan udføres i O(N9) tid.

For generelle M×N kort er der også visse nødvendige betingelser for flad foldbarhed, der kan testes i polynomiel tid. En gyldig foldning skal være i overensstemmelse med den partielle rækkefølge af paneler, der defineres af folderne. Hvis denne partielle rækkefølge indeholder cyklusser, er kortet ikke fladt foldbart.

---

 

Anvendelser i Den Virkelige Verden

 

Selvom kortfoldningsproblemet kan virke abstrakt og rent teoretisk, har det praktiske anvendelser. Et bemærkelsesværdigt eksempel er robotstøvsugere. Problemet for en robotstøvsuger, der skal støvsuge et gulv eller klippe en græsplæne, er at besøge hvert sted én gang og kun én gang uden at krydse sin egen sti. Den sædvanlige teknik for kommercielle robotstøvsugere er at bruge enten en spiral- eller et zigzag-mønster (også kaldet "booster feed-on"). Hvis et rum har forhindringer eller en irregulær form, opdeler algoritmen det i mindre rektangulære områder og bruger standardmønsteret for hvert.

Men i mange tilfælde skal robotten besøge bestemte "waypoints" i en specifik rækkefølge. I disse situationer er en simpel spiral eller zigzag ikke tilstrækkelig. Det er her, kortfoldning kommer ind i billedet. Et foldet stykke papir, set fra siden, kan give en optimal rute at følge. Rummet af alle mulige foldninger er netop generelt nok til at inkludere ruter, der besøger waypoints i forskellige rækkefølger, og præcist specifikt nok til, at det ikke tager for lang tid at søge. Når en robot finder en foldning, der matcher dens mål, kan den omdanne det til en sekvens af punkter på et gitter og gøre det til sin navigationsplan. Både spiral- og zigzagmønstrene er faktisk inkluderet i rummet af kortfoldninger, da de begge er gyldige måder at folde et stykke papir på.

---

 

Afsluttende Tanker

 

Kortfoldning, der ved første øjekast fremstår som et simpelt problem, viser sig at være dybt, subtilt og indviklet. På trods af årtiers forskning forbliver mange aspekter af det uløst, især for større og mere komplekse kort. Den fortsatte udforskning af dette felt afslører ikke kun fascinerende matematiske udfordringer, men også praktiske anvendelser inden for robotik og andre områder.

---

 

Spørgsmål til Eftertanke:

 

• Hvorfor er det så svært at finde en generel formel for antallet af foldninger for N×N kort?

• Hvilke uopdagede matematiske principper kunne potentielt låse op for en løsning på kortfoldningsproblemet for store N?

• Kunne de nuværende algoritmer for 2×N kort, som reducerer problemet til et "hidden tree problem", generaliseres til M×N kort?

• Hvilke nye anvendelser kunne dukke op, hvis vi kunne beregne foldninger for vilkårligt store kort hurtigt?