Fold og Klip Teoremet:
Magien ved ét snit

Forestil dig, at du kan tage et helt almindeligt stykke papir, folde det på en bestemt måde, og derefter klippe med et enkelt, lige klip gennem alle lagene. Når du folder papiret ud igen, har du klippet en hvilken som helst ønsket form ud – uanset hvor kompliceret formen er!
Dette lyder måske som magi, men det er faktisk virkeligheden bag et fascinerende matematisk resultat kendt som Fold og Klip Teoremet. Teoremet kaldes formelt også "Fold and One-Cut Theorem".Hvad siger teoremet?
Teoremet siger, at enhver form, der udelukkende er afgrænset af lige linjer kan klippes ud af et enkelt stykke papir med kun ét lige klip.
Dette gælder under teoretiske betingelser, hvor papiret er uendeligt tyndt, og folderne kan laves med perfekt præcision, uden at papiret går i stykker. Dette overraskende resultat betyder, at man f.eks. kan folde et stykke papir og med et enkelt klip skære alle bogstaver i alfabetet ud på én gang (hvis de er tegnet med lige linjer foldet korrekt).
Hvordan er dette muligt? Hemmeligheden bag foldningen
Hemmeligheden ligger i den måde, papiret foldes på før klippet. Målet er at folde papiret helt fladt, så alle de linjer, du ønsker at klippe langs, præcist ligger oven på hinanden langs en enkelt, lige linje.
Nøglen til denne foldning er et geometrisk mønster, der kaldes straight skeleton (lige skelet).
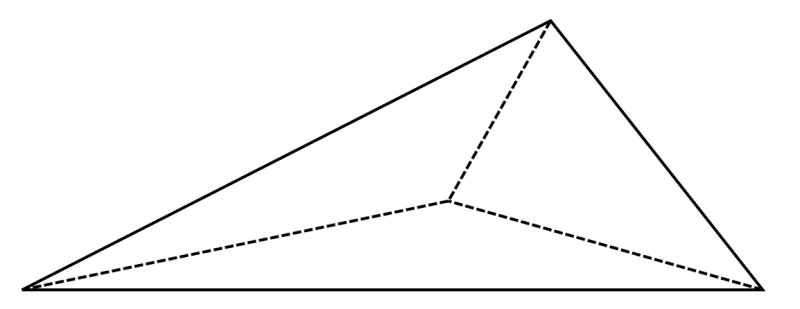
Et Straight skeleton-mønster er et sæt af foldelinjer, der skabes på papiret - et "foldernes skelet", der skal guide foldningen.
- Forestil dig den form, du ønsker at klippe ud.
- Nu skal du forestille dig, at denne form langsomt begynder at "skrumpe" indad. Kanterne på formen bevæger sig indad, men forbliver parallelle med deres oprindelige position og bevæger sig med samme hastighed.
- Efterhånden som formen skrumper, vil dens hjørner bevæge sig og til sidst mødes.
Matematisk set består straight skeletonet af linjesegmenter, der er dele af de vinkelhalveringslinjer, der dannes mellem de linjer, du ønsker at klippe (disse ønskede klippelinjer kaldes i denne sammenhæng for "grafkanter").
Fra Skelet til Ét Enkelt Klip: Den Fuldstændige Foldning
Selve foldeprocessen bygger altså på dette straight skeleton, hvor folder laves langs skelettets linjer. Det viser sig dog, at det lige skelet alene sjældent er tilstrækkeligt til at folde papiret helt fladt på den nødvendige måde. Derfor skal der tilføjes yderligere folder, som viser sig at være vinkelrette folder til grafkanterne. De udgår fra hvert knudepunkt i straight skeletonet og møder de oprindelige ønskede klippelinjer i en ret vinkel. Når man folder langs både straight skeletonets linjer og disse vinkelrette folder, er det muligt at opnå en flad konfiguration, hvor alle de linjer, der skal klippes, er justeret perfekt.
Efter at have udført alle disse præcise folder, ligger papiret i en tilstand, hvor det ønskede snitmønster er stablet, så alle segmenter ligger langs en enkelt lige linje. Nu kan du tage din saks og foretage det ene, lige klip gennem alle lagene af papir. Når papiret foldes ud igen, vil det præcist matche den ønskede form.
For komplekse former kan det være matematisk og beregningsmæssigt udfordrende at konstruere det præcise straight skeleton og de nødvendige vinkelrette folder. Dette gøres ofte ved hjælp af computerprogrammer. I praksis ved vi fx, at det samtidig kan synes umuligt at klippe igennem mange lag med en saks. Så det er en god ide, at øve sig på meget simple figurer.


Fra Abstraktion til Håndgribelig Geometri
Fold og Klip Teoremet er et smukt eksempel på, hvordan abstrakt matematik og geometri kan føre til overraskende og elegante resultater under ideelle, teoretiske forhold. Det illustrerer origamiens dybe forbindelse til matematiske principper som geometri, mønstre og præcision.
For undervisere tilbyder teoremet en motiverende og intuitiv indgangsvinkel til at gøre abstrakte matematiske koncepter håndgribelige og visuelle for eleverne. Gennem praktiske foldeteknikker skaber eleverne taktile og visuelle repræsentationer af grundlæggende geometriske elementer som punkter, linjer, vinkler og former, hvilket kan styrke deres forståelse og udvikle det tilhørende matematiske sprog.
At tackle figurer som en stjerne eller en simpel firkant kræver relativt få folder baseret på symmetri og grundlæggende vinkelhalveringer. Mere komplekse figurer kræver en kombination af teknikker, herunder både vinkelhalveringer og vinkelrette folder. At arbejde med disse udfordringer er i sig selv en øvelse i problemformulering og -løsning.


Erik Demaine er anerkendt som den førende forsker inden for fold-og-klip teoremet.
Et nøgleværktøj i Damaines arbejde er konceptet om et strej-skelet (straight skeleton), hvor vinkelhalveringslinjerne bevæger sig indad, indtil de mødes. Disse linjer danner skelettet og styrer foldemønstret. Foldningsprocessen kræver præcision og strategisk tænkning og ofte arbejder man baglæns fra den ønskede form til foldningssekvensen.
Her kan du se og printe flere hans imponerende fold-og-klip-figurer
One cut-bogstaver: Erik Demaine har også lavet en side hvor du kan skrive tekst og printe fold-og-klip-skabeloner til bogstaverne fra a til z: Fold-cut-fonts
Historie
Fold-og-klip-teknikkens historie strækker sig flere århundreder tilbage. I 1721 instruerede den japanske bog Wakoku Chiyekurabe læsere i at skabe et japansk våbenmærke, sangaibisi med et enkelt klip.Teoremet blev først for alvor introduceret i 1960 af Martin Gardner gennem hans "Mathematical Games"-serie i Scientific American.
Et sjovt eksempel er, at udbryderkongen Harry Houdini startede som tryllekunstner og faktisk optrådte med at klippe en femtakket stjerne ud med et klip. Han udgav også bogen Paper Magic.
Amerikansk historie tilføjer en interessant vinkel. En artikel fra 1873 i Harper's New Monthly Magazine beskriver, at den amerikanske møbelpolstrer Betsy Ross viste teknikken for præsidenten George Washingtonde da de femtakkede stjerner skulle syes til det amerikanske flag. Anvisninger på disse stjerner findes på ushistory.org.

Denne Numberphile-video fortæller også om teoremet: