De magiske 60 grader
Hvordan kan en papirstrimmel, foldet med en helt vilkårlig vinkel til at starte med, ende med at skabe næsten perfekte ligesidede trekanter?'
Ligegyldig hvilken vinkel som du starter med!

Sådan gør du:
- Første fold (vilkårlig): Start med en papirstrimmel. Fold den nedad og lav en helt tilfældig vinkel ved strimlens nederste venstre hjørne. Fold derefter papiret ud igen. Denne første foldelinje er dit udgangspunkt.
- Anden fold: Fold nu strimlen igen, så den præcist flugter med din første foldelinje. Dette skaber en ny foldelinje.
- Gentagelse: Fortsæt med at folde på samme måde, skiftevis opad og nedad, og altid sørg for, at din nye foldelinje flugter præcist med den senest dannede foldelinje.
Nu viser det sig, at uanset hvilken vinkel, som man starter med, vil strimlen altid ende med at skabe vinkler meget tæt på 60 grader.

På denne strimmel er den første vinkel 45 grader. Den markerede trekants vinkel er på 59.9853515625 grader.
Den matematiske forklaring
For at forstå dette anvendes en matematisk model:
-
Definition af vinkler: Lad os sige, at papirstrimlen ligger vandret. Den første fold skaber en vinkel, vi kalder θ1 (theta 1), ved den nederste venstre del af strimlen langs bundkanten.
-
Vinkeldeling ved anden fold: Når du laver den anden fold ved at flugte papiret med den første fold, halverer denne fold en vinkel, som vi kan kalde for 2α (to alfa), der er lig med 180º - θ (hvor θ er vinklen fra den forrige fold).
-
Geometrisk set viser det sig, at α er lig med den næste vinkel, θ2 (theta 2).
Her er første fold lavet på 45 grader.
Den nye foldelinje skaber en vinkel α, som er:
α = (180 - θ) / 2
α = 90 - (θ / 2)
Denne formel fortæller os, at hver ny vinkel θn er resultatet af 90 grader minus halvdelen af den foregående vinkel θn-1.
Ny vinkel = 90 grader - (Gammel vinkel / 2)
Ovenstående formel kaldes for en forholdsformel og vi har nu fundet dén som gælder for øvelsen med papirstrimlen:
Forholdsformlen:

Eksempel for en vinkel på 100 grader:
vinkel 1 Lad os antage, at den første vinkel er 100 grader.
Så bliver vinkel 2 = 90 - (100 / 2) = 40 grader. (20 grader fra 60)
Vinkel 3 = 90 - (40 / 2) = 70 grader. (10 grader fra 60)
Vinkel 4 = 90 - (70 / 2) = 55 grader. (5 grader fra 60)
Vinkel 5 = 90 - (55/ 2) = 62,5 grader. (2 grader fra 60)
Vinkel 6 = 90 - (62,5 / 2) = 58,75 grader. (1,25 grader fra 60)
Vinkel 7 = 90 - (58,75 / 2) = 60,625 grader. (0,625 grader fra 60)
Vinkel 8 = 90 - (60,625 / 2) = 59,6875 grader. (0,3125 grader fra 60)
Vinkel 9 = 90 - (59,6875 / 2) = 60,15625 grader. (0,15625 grader fra 60)
Vinkel 10 = 90 - (60,15625 / 2) = 59,921875 grader. (0,078125 grader fra 60)
Går altid mod 60 grader!
Konvergens og iteration:
Det mest bemærkelsesværdige ved denne sekvens af vinkler (θ1, θ2, θ3, ...) er, at den konvergerer mod 60 grader. Det betyder, at jo flere gange du folder papiret, jo tættere kommer vinklerne på at være præcis 60 grader.
En talrække siges at konvergere, hvis dens tal kommer tættere på en grænseværdi, når rækken forlænges.
Man kan også bruge ordet iteration om en gentagen proces, der gradvist nærmer sig en løsning. Det bruges til komplekse problemer, hvor direkte løsninger er svære, fx i numerisk analyse for at finde tilnærmede ligningsrødder eller løse differentialligninger.
Analyse af ligningen:

Ligningen beskriver et rekursivt forhold. Det kan vi konkludere, da værdien af 𝜃𝑛 afhænger af den foregående værdi (𝜃𝑛−1).
1) Analyse med iteration:
Hvis vi har en startværdi som basisscenarie, kan vi løse ligningen for forskellige stadier af 𝜃.
Oftest gives en startværdi i denne type problemer. Lad os f.eks. sige 𝜃0 er givet (f.eks. 𝜃0 = 90).
Indsæt 𝜃0 = 90 i ligningen for at finde 𝜃1:
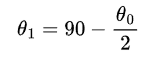
Herved får vi at 𝜃1 = 45
Fortsæt denne proces for at finde efterfølgende værdier:
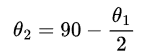
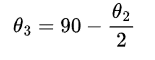
og så videre.
Ved at beregne et par led kan du begynde at bemærke et mønster, der kan hjælpe med at generalisere løsningen.
2) Analyse af konvergensværdi:
Da ligningen har en karakteristik, der kan føre til konvergens, kan du analysere grænsen for konvergens-værdien for 𝜃𝑛, som 𝑛 nærmer sig uendeligheden. Lad os kalde denne værdi for L
Her findes der en smart metode: Du kan sætte både 𝜃𝑛 = L og 𝜃𝑛−1 = L i den oprindelige ligning for at finde konvergensværdien:

Konklusion
Med en specifik startværdi kan du således bruge denne rekursive formel til at beregne 𝜃𝑛 trin for trin, og du kan analysere sekvensens opførsel for at finde ud af, at den konvergerende værdi.

