
Potenser
Potenser er et af matematikkens mest fundamentale og kraftfulde koncepter. De gør det muligt at udtrykke meget store eller meget små tal på en enkel og kompakt måde.
Hvad er en potens?
Potenser er en kortfattet måde at skrive gentagen multiplikation på.
En potens består altid af to dele:
- Et grundtal: Det store tal, der ganges med sig selv.
- En eksponent (eller potens): Det lille hævede tal, der angiver, hvor mange gange grundtallet skal ganges med sig selv. Tænk på eksponenten som en "tæller" for gentagelserne.

Eksempel: I udtrykket 2⁵ er 2 grundtallet og 5 eksponenten. Dette betyder 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 =
Et andet eksempel: I 3² er 3 grundtallet og 2 eksponenten. Dette betyder 3 ⋅ 3 = 9. Vi siger ofte, at 3² er "3 i anden" eller "3 kvadreret".
"I anden" og "I tredje" har egne navne
- "I anden" (eksponent 2): Grundtallet ganges med sig selv to gange, f.eks. 5² = 5 ⋅ 5 = 25. Dette svarer til arealet af en kvadrat. En kvadrat med sidelængde 5 har arealet 5² = 25 kvadratenheder. Derfor kaldes det at "kvadrere" et tal.
- "I tredje" (eksponent 3): Grundtallet ganges med sig selv tre gange, f.eks. 4³ = 4 ⋅ 4 ⋅ 4 = 64. Dette kaldes at "kubere" et tal, da det svarer til volumen af en kube. En kube med sidelængde 4 har volumenet 4³ = 64 kubikenheder.
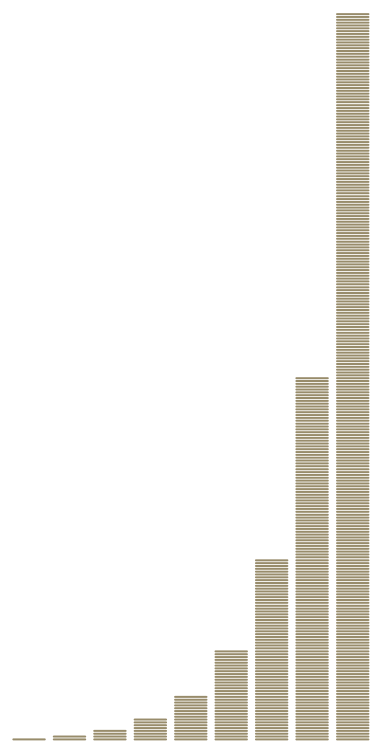
Papirfoldning og Eksponentiel Vækst
Potenser beskriver fænomener med eksponentiel vækst – vækst, der vokser hurtigere og hurtigere. Papirfoldning er et klassisk eksempel på dette:
- Start: 1 lag papir.
- 1. foldning: 2 lag ()
- 2. foldning: 4 lag (2²)
- 3. foldning: 8 lag (2³)
- 4. foldning: 16 lag (2⁴)
For hver foldning fordobles antallet af lag. Hvis du folder et stykke papir gange, vil antallet af lag være 2n.
Eksempler på den hurtige vækst:
- Efter 10 foldninger: 2¹⁰ lag (ca. tykkelsen af en længere roman).
- Efter 20 foldninger: 2²⁰ lag (over en million lag – tæt på 100 meter tykt!).
- Efter 42 foldninger: 2⁴² = 4.398.046.511.104 lag der teoretisk vil kunne nå Månen (ca. 384.400 km)!
- Med 49 foldninger kommer du til Venus
-
Til Sirius (den klareste stjerne på nattehimlen) folder.
- Kanten af det observerbare univers folder
Dette eksempel viser tydeligt, hvor kraftfulde potenser er, og hvor hurtigt tal kan vokse.
Rækkefølgen: 2, 4, 8, 16, 32, 64, 128 ... kaldes for en geometrisk progression.
Hvad er en geometrisk progression?
En talrække, hvor hvert tal findes ved at gange det forrige med det samme tal hver gang, kaldes for en geometrisk progression.
I rækken 2, 4, 8, 16 … ganger med 2 hver gang. I rækken 3, 9, 27, 81, … ganger vi med 3 hver gang.
Geometriske rækker er nyttige i mange områder som matematik, økonomi, fysik og IT, når vi skal beskrive noget, der vokser eller falder hurtigt. Du kan finde et hvilket som helst tal i rækken ved hjælp af en simpel formel:
an = a1 × kn-1
Her er an det ønskede led, a1 det første led, k kvotienten, og n leddets nummer.
Eksempel på udregning med formlen:
Find tykkelsen af 10 foldninger: Hvis vi bruger eksemplet med papirfoldning vil vi med formlen for geometrisk progression altid kunne finde en given tykkelse efter enhver foldning. Forestil dig, at du har et standardark papir, som er cirka 0,1 millimeter tykt. Hver gang du folder papiret, fordobles antallet af lag, altså tykkelsen. Dette scenarie kan beskrives ved: an = a1 · kn-1
Her er an tykkelsen efter n foldninger, a1 er starttykkelsen (0,1 mm), og k er fremskrivningsfaktoren (i dette tilfælde 2, da tykkelsen fordobles ved hver foldning).
Lad os sige, at du folder papiret 10 gange. Udregningen ser således ud:
- a1 = 0,1 mm
- k = 2
- n = 10
Ved indsættelse i formlen får vi:
a10 = 0,1 · 210-1 = 0,1 · 29
Da 29 er 512, bliver resultatet:
a10 = 0,1 · 512
a10 = 51,2 mm
Efter 10 foldninger vil papiret altså være 51,2 millimeter tykt, svarende til lidt over 5 centimeter. Det kan altså hurtigt føre til ekstremt store værdier, når antallet af gentagelser øges.
Hvor mange gange kan du folde et papir?
Har du prøvet, hvor mange gange du kan folde et almindeligt stykke A4-papir? De fleste vil opdage, at de efter 6-7 foldninger må give op. Papiret er blevet for tykt og for lille til at fortsætte. Dette er ikke bare en praktisk demonstration af eksponentiel vækst med potenser., men også en sjov udfordring.
Hvorfor er det så svært?
Hver fold fordobler lagene og halverer arbejdsfladen. Efter 7 fold har du 2⁷ = 128 lag papir! Tykkelsen bliver så stor, at det fysisk umuliggør endnu en fold. Denne grænse har længe skabt myten om, at man ikke kan folde papir mere end 7-8 gange. Men som mange andre myter er den blevet udfordret.
Verdensrekorden i papirfoldning
I 2002 beviste gymnasieeleven Britney Gallivan, at det var muligt at bryde foldningsgrænsen. Hun foldede et enkelt stykke papir hele 12 gange og satte dermed en Guinness Verdensrekord.
Hvordan? Ved at tænke kreativt. I stedet for almindeligt papir brugte hun en 1,2 kilometer lang rulle toiletpapir. Dette ekstremt lange, tynde materiale gjorde det muligt at opnå 2¹² = 4096 lag.
Britney udviklede også matematiske formler for, hvor langt eller bredt papir skal være for at foldes et bestemt antal gange.

Se MythBusters forsøge at slå rekorden her:
For at simplificere udregninger med potenser findes der en række regler. De kan de spare dig for meget tid, når først man forstår dem.
Potensregler:
Potenser med eksponent 0
Ethvert tal (undtagen 0) opløftet i 0. potens er altid 1.
a⁰ = 1
( Hvor a ≠ 0 )
Hvorfor? Forestil dig . Ved hjælp af divisionreglen (Regel 2) får vi . Men vi ved også, at et tal divideret med sig selv er 1. Derfor må .
Multiplikation af potenser med samme grundtal
Når du ganger potenser, der har det samme grundtal, skal du lægge eksponenterne sammen.
aᵐ ⋅ aⁿ = aᵐ⁺ⁿ
Division af potenser med samme grundtal
Når du dividerer potenser, der har det samme grundtal, skal du trække eksponenterne fra hinanden.
aᵐ / aⁿ = aᵐ⁻ⁿ
( Hvor a ≠ 0 )
Potenser med negativ eksponent
En negativ eksponent betyder, at du skal tage reciprokken af grundtallet opløftet i den positive eksponent.
a⁻ⁿ = 1 / aⁿ
( Hvor a ≠ 0 )
Hvorfor? Vi kan se det ud fra division:
Potens af en potens
Når du har en potens, der er opløftet i endnu en potens, skal du gange eksponenterne sammen.
(aᵐ)ⁿ = aᵐ*ⁿ
Brøk opløftet i en potens
Når en brøk opløftes i en potens, kan du opløfte tælleren og nævneren hver for sig i potensen.
(a / b)ⁿ = aⁿ / bⁿ
( Hvor )