Oversigt over metoder til at opdele et papir

 

Mange origamidesigns starter med at dele papiret i lige store dele.

Der findes rigtig mange måder at gøre det på. Her er en række mere enkle måder at dele papir i delene:

3 - 5 - 6 - 7 - 9 - 10 - 11 - 12 og 13

 

Vejledning

  • Klik på billederne for at forstørre dem.
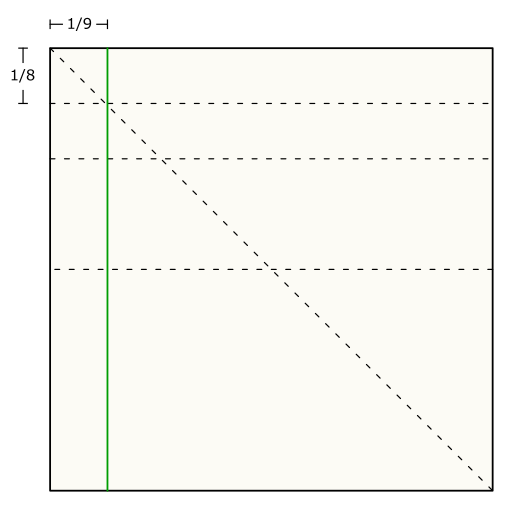
  • Start med de binære foldelinjer, der deler papiret i 2, 4, 8 eller 16 dele.
  • Fold derefter diagonalt.

 

  • Den grønne linje viser hvor to foldelinjer skærer hinanden i en ønsket afstand.

Den ønskede afstand.

  • Vil du fx dele papiret i 13.dele, vil den grønne linje dele papiret i 5/13 og 8/13.
  • Start da med at folde de 8/13 og brug folderne herfra som afstande, der kan hjælpe med folde resten af papiret.

Fold ikke hele papiret

  • Prøv at undgå at folde papiret unødigt, da færre foldelinjer vil resulterer i et pænere og mere stabilt slutprodukt.

3-deling

5-deling

6-deling

Start med at dele i 3.-dele.

Halver herefter 3.delene

7-deling

9-deling

10-deling

Start med at dele i 5.dele. Halver herefter 5.-delene.

11-deling

13-deling

Algebraiske beviser

Bevis for 1/5

Lad kvadratet (ABCD) have sidelængde 1 med hjørnerne:

A(0, 1), B(1, 1), C(0, 0), D(1, 0).

  1. Foldelinje 1: diagonalen AD: Ligningen er y = 1 − x.

  2. Foldelinje 2: går gennem C(0, 0) og punktet P(1, 0.25).

Punkterne sættes ind i formlen: m = (y2 - y1) / (x2 - x1) 

Hældningen er m = (0.25 − 0)/(1 − 0) = 0.25.
Dermed: y = 0.25x.

  1. Skæringspunktet findes ved at sætte ligningerne lig hinanden:
     1 − x = 0.25x
     ⟹ 1 = 1.25x
     ⟹ x = 0.8

Indsæt i y = 0.25x: 

y = 0.25 × 0.8 = 0.2.

  1. Skæringspunktet er derfor
      S = 0.8, 0.2.

Konklusion

Punktet ligger (y = 0.2) over bunden — altså 1⁄5 af papirets højde, som ønsket.

Formlen til at finde hældningskoefficient

Hældningskoefficienten beregnes ud fra to punkter på linjen med formlen: m = (y2 - y1) / (x2 - x1),

hvor m er hældningskoefficienten, (x1, y1) og (x2, y2) er punkternes koordinater.